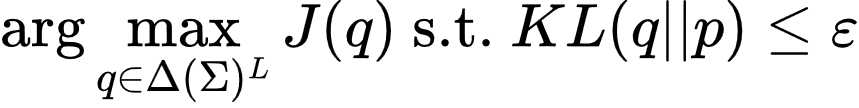Watermarking Diffusion Language Models

Why is watermarking Diffusion LMs challenging?

With traditional autoregressive language models (ARLMs), most watermarking schemes rely on previously generated tokens (i.e., the context) to decide how to watermark the next token. For instance, Red-Green watermarks (illustrated here) hash the context to partition the vocabulary into a green and a red set. Then, the model is biased to sample tokens from the green set. For detection, the watermark detector counts the number of green tokens in a given text, and if this number is significantly higher than random chance, the text is declared watermarked.

Why watermarking Diffusion LMs is challenging

Diffusion Language Models (DLMs) generate tokens in arbitrary order by iteratively unmasking a sequence of masked tokens (i.e., tokens yet to be generated). Importantly, this means that when generating a given token, other tokens in its context may not yet have been generated. Hence, the watermarking scheme cannot compute the hash of the context to determine the green and red sets. Thus, when generating such tokens, we cannot bias the distribution toward the green set, which weakens the watermark. This means that we need to design a new watermark that can handle masked tokens in the context.

Our watermark for Diffusion LMs

For every masked token, while we cannot compute its hash, the DLM still provides us with a probability distribution over the vocabulary. Hence, our key insight is to leverage this distribution over the hashes of the context to determine how much we can bias the distribution.

Specifically, as illustrated above, when computing the watermarked distribution for a masked token, we take into account two factors: (i) we apply the existing Red-Green watermark in expectation over the hashes of the context, and (ii) we bias the distribution towards tokens that lead to hashes making other tokens green. While the first term is a natural extension of the Red-Green watermark, the second term is specific to the order-agnostic generation of DLMs and allows making tokens already generated green.

Because our watermarking scheme is based on the same idea as the Red-Green watermark, we can use the same watermark detector for detection. Given a text, the watermark detector counts the number of green tokens in the text and performs a binomial test to determine whether the number of green tokens is significantly higher than random chance. If this is the case, the text is declared watermarked.

Demo

The demo below shows how the watermarking algorithm transforms the logits distribution of a DLM into a watermarked distribution. We start with a partially masked sequence (I [?] [?] [?] pizza.). For each masked token, the DLM returns a distribution over the vocabulary. Then, we illustrate how our watermarking scheme modifies this distribution using the two terms described above to obtain the watermarked distribution.

Deriving our watermark from theoretical principles

To formalize our watermark algorithm and justify the importance of the two terms in the watermarked distribution, we provide a theoretical analysis of our watermarking scheme. In particular, we consider watermarking as a constrained optimization problem: the goal of the watermark is to distort the original model probability distribution p (factorized over a sequence of size L) into a distribution q that maximizes the number of green tokens generated without significantly impacting the quality of the generated text. We denote this expected number of green tokens as J(p). As a proxy for text quality, we consider the Kullback–Leibler divergence between the original and watermarked distributions.

Watermarking as a constrained optimization problem

This optimization problem admits an (almost) closed-form solution: the optimal watermarked distribution q* is obtained by adding to the logits of the original distribution p a term proportional to the gradient of J(p). The proportionality coefficient δ is a parameter that controls the strength of the watermark. We derive from this result the watermark algorithm described on the left. The remaining technical challenge is to compute J(p) efficiently. We show that, with most hash functions, J(p) can be computed efficiently.

With this theoretical approach, however, interpreting how the watermark operates is challenging. Yet, if we look more closely at the gradient of J(p), we can recover the two terms of our watermarking scheme introduced above. This means that our watermarking scheme is not only intuitively understandable but also theoretically grounded, as it is optimal with respect to our optimization problem!

Interpretation of our watermark — **Remarks:** G is a matrix where each entry indicates the color (green or red) of a token given a hash. The vector h is the distribution over the hashes of the context. The function H is the hash function. Lastly, Ω is the random text being generated. The equation is hard to parse at first sight, but it is actually quite intuitive. The first term is indeed the expectation of the color over the hashes of the context. In the second term, we look, for every token in the context of the token being generated, which concrete value (of the token being generated) would yield hashes that make them green, and we weight this by a corresponding probability. Computing this sum "manually" is tedious to implement, but thanks to our theoretical analysis, we can derive it automatically with backpropagation! If we had not performed this theoretical analysis, it would have been difficult to come up with an easy-to-implement algorithm that computes this second term.

Evaluation of our watermark

We evaluate our watermarking scheme on two DLMs: Llada-8B and Dream-7B, and compare it to a naive adaptation of the Red-Green watermark for DLMs (i.e., applying the Red-Green watermark only when the context is fully unmasked). We find that our watermark is significantly more effective than this naive adaptation, and that, on reasonably small text, it achieves over a 99% true positive rate with minimal impact on text quality!

We also evaluate the robustness of our watermark against various attacks, including text editing (deletion, insertion, substitution), paraphrasing with LLMs, and back-translation. We find that our watermark is comparably robust to established ARLM watermarking schemes.

Citation

@misc{gloaguen2025watermarkingdiffusionlanguagemodels,
      title={Watermarking Diffusion Language Models}, 
      author={Thibaud Gloaguen and Robin Staab and Nikola Jovanović and Martin Vechev},
      year={2025},
      eprint={2509.24368},
      archivePrefix={arXiv},
      primaryClass={cs.LG},
      url={https://arxiv.org/abs/2509.24368}, 
}